RD waves around obstacles

In this computational project, we  investigate how initially planar reaction-diffusion (RD) wavefronts interact with obstacles. RD waves propagate around no-flux boundary objects within a channel and create cusps when the two separated sections on the downstream side collide. The curvature dependent wave velocity enables the wave to straighten again due to the higher velocity of negatively curved sections, and within the cusp, as shown in the stroboscopic view of a single wavefront at constant time intervals propagating left-to-right around a tilted triangle. This is primarily a summer research project in collaboration with John Lindner. With his experience in Objective-C coding, we developed programs to simulate RD waves propagating in a two-dimensional excitable system (channel) using the realistic two-variable Tyson-Fife model for chemical RD waves.

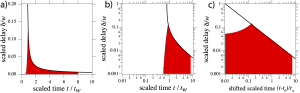
Vincent Hui ’19 started exploring various possibilities and Nate Smith ’18 developed, in his Senior I.S., an Objective-C code to simulate propagating RD waves in 2D channels. Besides placing ‘simple’ triangles, rectangles, and ellipses as obstacles in a channel, he implement the use of any binarized image/object to investigate the propagation behavior through such a system. With Rebecca Glaser’s work during the 2018 summer research program, we could show that the initially planar wavefront (or iso-concentration line) is restored after a relaxation period that can be characterized by a power-law. The delay is the difference between the leftmost wave section, if interacting with an obstacle, and the position along the x-axis of an undisturbed wave in the channel.

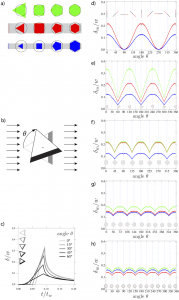A beautiful result was the cyclic delay as the obstacle orientation changes and the effect of constant area (green), constant cross section (red) and constant side length (blue) of n-sided polygons. The maximum delay function of the obstacle orientation θ within the channel for for objects (line, triangle, square, pentagon, and hexagon) is shown in the figure.

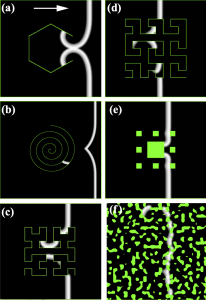During the 2019 summer, Yang (Fish) Yu explored the behavior of reaction-diffusion wavefronts encountering various shapes beyond the previous solid, convex obstacles. As previously simulated, waves begin along the vertical left boundary and have a general rightward motion through the channel. But the wave motion around/through the concave polygons (“open” with one side missing), Archimedean spirals, Hilbert curves, Peano curves, Sierpinski carpets, and Perlin-noise-generated randomness showed a much larger variety of behavioral patterns. Concave, spiral, and especially fractal obstacles can sustain wavefronts locally for very long times. Spiral obstacles can sustain wavefront motion for long times, limited in practice by the narrowness of the spiral walls and the width of the channel which allows the RD to propagate. Fractal obstacles can support extended motion of many wavefront segments in fascinating patterns, again limited mainly by the narrowness of their maze-like features.

Senior Independent Study theses
  • Nate Smith ’18: A computational simulation of Belousov-Zhabotinsky wave behavior around obstacles
NSF-REU Summer research
  • Chase Fuller (2019, Sherman Fairchild grant): 3D Graphics, Parallel Processing, and Heterogeneous Media with the Photosensitive Tyson-Fife Model
  • Yang (Fish) Yu (2019, Sherman Fairchild grant): Reaction-diffusion wavefronts interacting with obstacles
  • Rebecca Glaser – SUNY Geneseo, NY (2018): Simulation of Reaction-Diusion Waves Interacting with Convex Obstacles
  • Wan Hang (Vincent) Hui (2017): A Computational Analysis for BZ Reaction-Diusion Waves with Obstacles
Oral presentations
  • Chase Fuller: “Chemical diode behavior in the Belousov-Zhabotinsky reaction due to inhomogeneous diffusion“, Fall 2019 Meeting of the APS Ohio-Region Section, Flint, MI, 2019 October 11-12
  • Yang (Fish) Yu: “Reaction-diffusion wavefronts with concave, spiral, fractals and soft obstacles“, 47th Annual Mathematics Conference: Differential Equations and Dynamical Systems and their Applications, Miami University, Oxford, OH, 2019 September 20-21
  • Chase Fuller: “Chemical diode behavior in the Belousov-Zhabotinsky reaction due to inhomogeneous diffusion“, 47th Annual Mathematics Conference: Differential Equations and Dynamical Systems and their Applications, Miami University, Oxford, OH, 2019 September 20-21
Poster presentations
  • F. Yu, J.F. Lindner, and N. Manz: “Reaction-diffusion around concave, spiral, fractal, and soft obstacles” Fall 2019 Meeting of the APS Ohio-Region Section, Flint, MI, USA, 2019 October 11-12.
  • R. Glaser, N. Smith, V.W.H. Hui, J. Lindner, and N. Manz: “Disruption and Recovery of Reaction-Diffusion Wavefronts Colliding with Obstacles” Spring 2019 Meeting of the APS Ohio-Region Section, Wooster, OH, USA, 2019 March 29-30
  • N. Smith, R. Glaser, V.W.H. Hui, J. Lindner, and N. Manz: “Reaction-diffusion wavefronts colliding with obstacles” Fall 2018 Meeting of the APS Ohio-Region Section, Toledo, OH, USA, 2018 September 2-3
  • N. Smith, J. Lindner, and N. Manz: “A Computational Simulation of Belousov-Zhabotinsky Wave Behavior around Obstacles” Spring 2018 Meeting of the APS Ohio-Region Section, East Lansing, MI, USA, 2018 March 23-24
  • V.W.H. Hui, J. Lindner, and N. Manz: “The effect of obstacles on the propagation speed of reaction-diffusion waves” Fall 2017 Meeting of the APS Ohio-Region Section, Oxford, OH, USA, 2017 October 13-14
  • A. Gould and N. Manz: “BZ-Reaction diffusion wave speed around obstacles” Spring 2017 Meeting of the APS Ohio-Region Section, Ypsilanti, MI, USA, 2017 May 5-6
Publications (click for more info)
  • Y. F. Yu, C. A. Fuller, M. K. McGuire, R. Glaser, N. J. Smith, N. Manz, and J. F. Lindner, Disruption and recovery of reaction-diffusion wavefronts interacting with concave, fractal, and soft obstacles, Physica A: Statistical Mechanics and its Applications  565 (2021), 125536.
  • N. J. Smith, R. Glaser, V. H. W. Hui, J. F. Lindner, and N. Manz, Disruption and recovery of reaction-diffusion wavefronts colliding with obstacles, Physica A: Statistical Mechanics and its Applications 517 (2019), 307-320.