Angular velocity of a rotating spiral
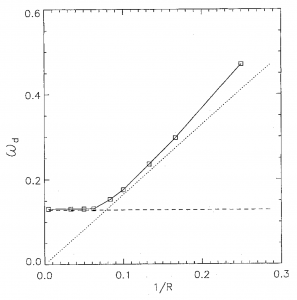
The higher the Gaussian curvature G of the non-planar system is, the faster a reaction-diffusion spiral wave will rotate (Brazhnik et al., Theor. Math. Phys. 74(3), 300-306 (1988), Zykov and Müller, Physica D 97(1-3), 322-332 (1996)). This relationship is shown in the figure, in which the angular velocity ω of a spiral wave is computed as a function of the inverse radius of a circular domain. Analytical estimates of this dependence for small radii (dotted line) and large radii (dashed line).
An indirect proof in Manz et al., Phys. Lett. A. 316(5), 311-316 (2003) needs to be complemented by a direct proof, actually measuring the angular velocity of rotating spirals on curved systems. Melita Wiles ’22 used a mold with various quasi-2D spherical shell caps and a liquid BZ solution and determined ω as a function of 1/R.
This project needs to be continued to proof that the Gaussian curvature G and not the ‘simple’ curvature K is driving the effect. Therefore, a comparison of the angular velocity of a planar system with surfaces of constant zero Gaussian curvature (cylinder, elliptic cylinder, cone, elliptic cone) is necessary.
Melita Wiles ’22 used two different existing molds to measure angular velocities of rotating spiral waves on surfaces with different Gaussian curvatures. Until now, the results are inconclusive. More experiments and improving the currently used BZ solution is needed.
Senior Independent Study theses
- Melita Wiles ’22: Angular frequency of rotating spiral waves in a chemical reaction-diffusion system
Poster presentations
- M. Wiles and N. Manz: “Angular frequency of rotating spiral waves in a chemical reaction-diffusion system” APS March Meeting 2022, Chicago, IL, USA (virtual), 2022 March 16
